Pythagorean Theorem Found On Clay Tablet 1,000 Years Older Than Pythagoras

For anyone who has delved into the world of mathematics, the name Pythagoras likely evokes both admiration and the occasional exasperated sigh. While Pythagoras is undoubtedly a monumental figure in the history of mathematics, it may come as a surprise that the equation most famously associated with him, a² + b² = c², was not his creation. Instead, it was unveiled centuries earlier, etched into an ancient Babylonian tablet known as IM 67118, which predates Pythagoras by a millennium.

This intriguing artifact serves as a testament to the profound mathematical knowledge possessed by the Babylonians, who utilized the Pythagorean theorem to determine the length of a diagonal within a rectangle. Dated to approximately 1770 BCE, long before Pythagoras’s birth around 570 BCE, this tablet was likely an instructional tool in teaching mathematics.

Further bolstering this revelation is another tablet from the period between 1800 and 1600 BCE. Adorned with a square and triangles, the tablet’s inscriptions, translated from the Babylonian base-60 counting system, unveil a deep understanding of the Pythagorean theorem, albeit not referred to by that name, as well as other intricate mathematical concepts.

Mathematician Bruce Ratner, in his research on this topic, concludes, “The Babylonians knew the relation between the length of the diagonal of a square and its side: d = square root of 2. This was probably the first number known to be irrational. However, this, in turn, means that they were familiar with the Pythagorean Theorem—or, at the very least, with its special case for the diagonal of a square (d² = a² + a² = 2a²)—more than a thousand years before the great sage for whom it was named.”

The question then arises: Why has the Pythagorean theorem been attributed to Pythagoras? The answer lies in the lack of surviving original writings from Pythagoras himself. Much of our knowledge about him has been passed down through the Pythagoreans, his followers and members of a secretive school he established in southern Italy, known as the Semicircle of Pythagoras. Within this circle, knowledge was transmitted orally due to the scarcity of writing materials. In reverence for their leader, many discoveries made by the Pythagoreans were ascribed to Pythagoras, ultimately resulting in the enduring term “Pythagoras’ Theorem.”

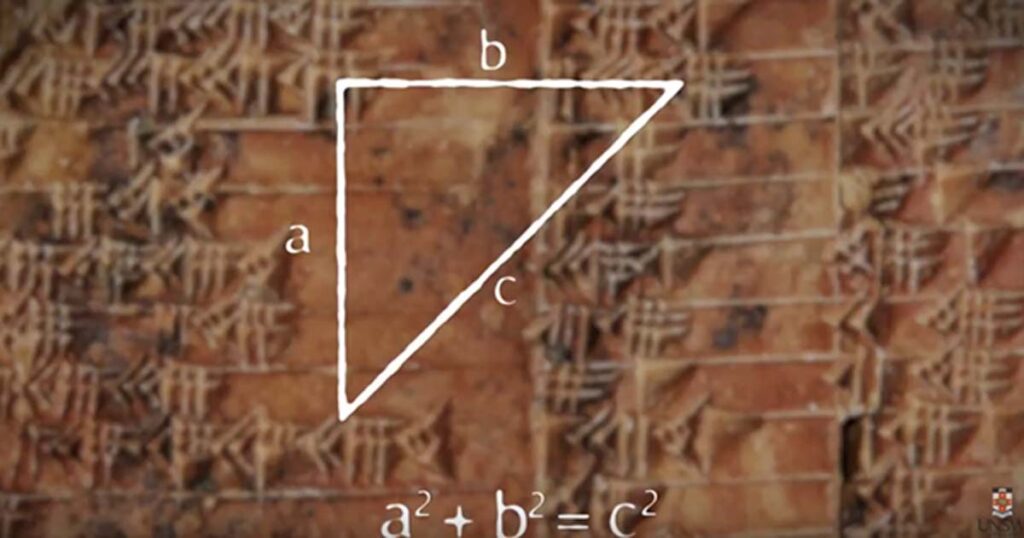
In the annals of mathematics, the Pythagorean theorem’s origins may be shrouded in the mists of time, but the enduring legacy of ancient Babylonian mathematicians is a testament to the enduring quest for knowledge that spans millennia.